7 Heaps
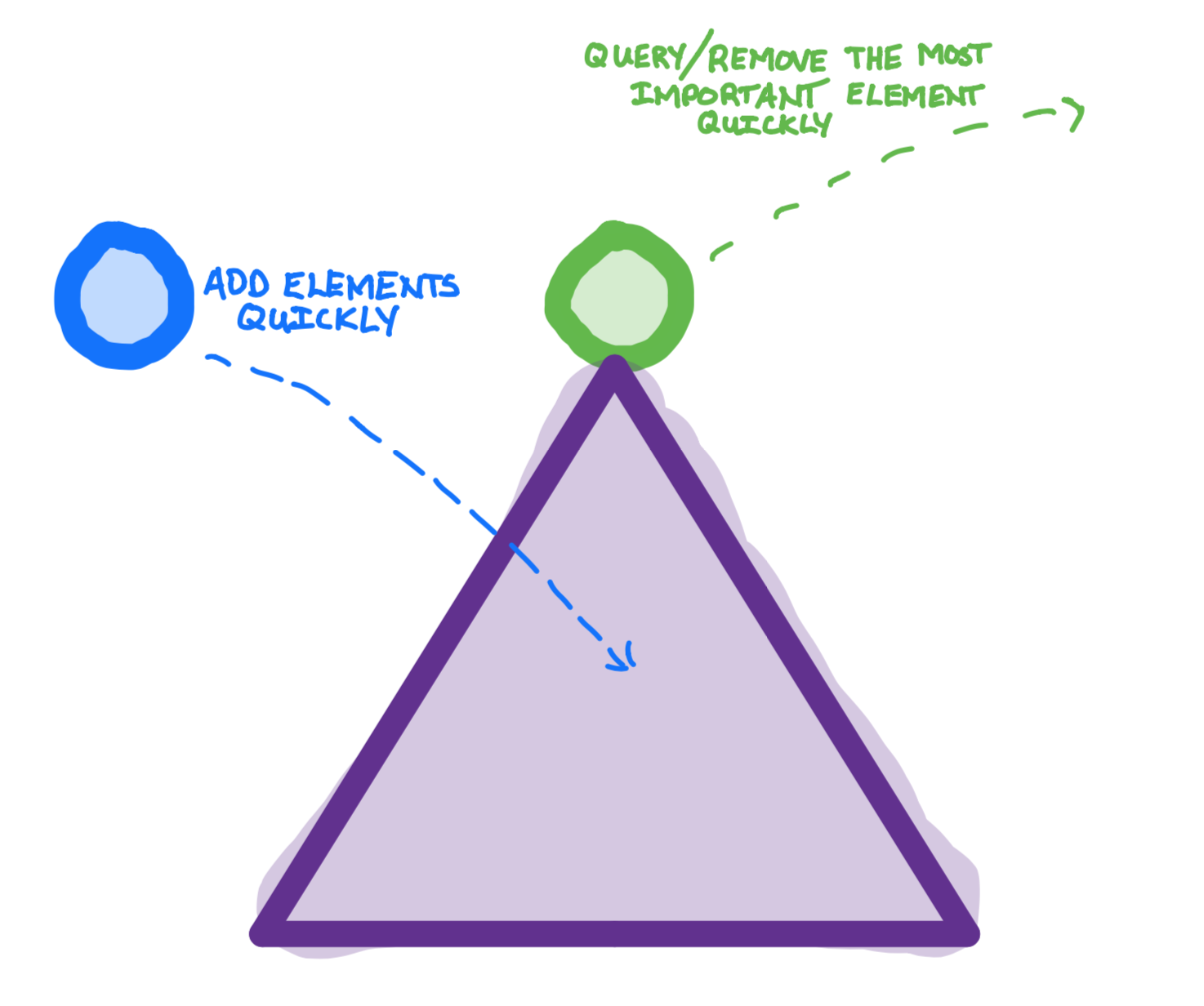
Heaps - Add elements quickly and query/remove the most important element quickly
7.1 Uses
getting the smallest/largest item each time in succession
maintaining top or bottom k elements, getting the median of large datasets
sorting data via heap sort
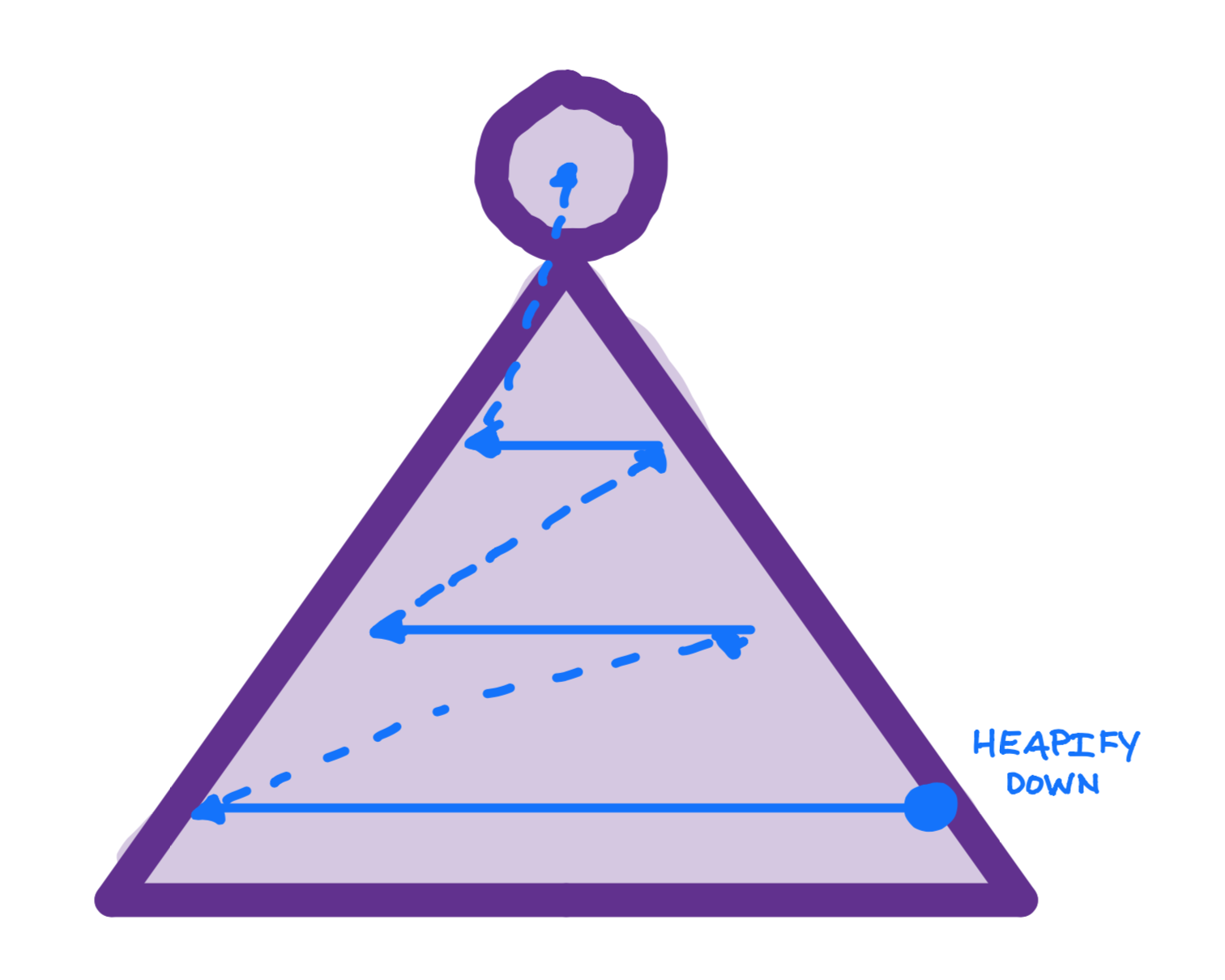
7.2 min heap vs max heap
min heap is smallest at top and higher at the bottom
max heap is the largest at top and goes smaller at the bottom
the logic is basically the same in either case, just inverted - we’ll do min heap here but the similar prinicples apply to max heap quite easily
7.3 Array based implementation
the simplest way to do it is with arrays that has each level contiguous
it makes swaps and indexing easy
not having to deal with pointers as much - we’re used to arrays
7.9 See also:
Learning to Love Heaps Long Medium Post by Vaidehi Joshi
Introduction to a Heap Video Series by Paul Programming
Old CS 225 resources page by Eddie Huang